先日(8月3日・4日)受講したクリエイティブシンキングセミナーにて学んだフレームワークを、何回かにわけてご紹介しようと思うシリーズ(←いつの間に!)の第3弾です。今回は一対比較を取り上げます。考え方としては実践していたかもしれませんが、こういう手法としてうかがったのははじめてでした。単純だけど、「目からうろこ」というか納得感は高かったです。
第1弾・第2弾は↓から。


一番おいしいと思うドーナツを決める
最近コンビニでも扱うようになったドーナツ🍩。ある4種類のうちどれがおいしいのかを、5名の総意で決める際にはどうすればよいでしょう?
5名全員がドーナツAがおいしいと思っているならば簡単ですが、個々が思うおいしいと思う店ついて確認したら「ドーナツA:2名、ドーナツB:2名、ドーナツC:1名」だった場合、どうやって総意が確定できるでしょうか?ドーナツC派の人が多少妥協して、ドーナツAかドーナツBに「鞍替え」して多数決にしたら、残された2名側にとって納得感は少ないでしょう。さらに、ドーナツC派の人が「2番目はドーナツDで、ドーナツAやドーナツBは論外」というならば、通常の話し合いでの収束は難しいでしょう。
その時に登場するのが一対比較です。
手法はとても簡単
いろいろなアイデアが出てきた時に、どれが最も優先度が高いと思っているのか、あるいは一番評価すべきポイントなのか・・・といったことが明確にならないことがあるかと思います。そういう時に、すべてのアイデアでいわゆる「総当たり戦」をして比較をしていき、その「勝ち点」を合計して点数を比較するだけです。
ドーナツの場合は、「ドーナツAとドーナツBならばどちらがおいしいか?」について、5名で多数決をとり、多数だった方に「1点」を与える。次に、「ドーナツAとドーナツCならば・・・」「ドーナツAとドーナツDならば・・・。」「ドーナツBとドーナツCならば・・・」というように総当たり戦を行います。そうすると、各ドーナツごとに得点が出てきます。例えば、以下のような表となります。
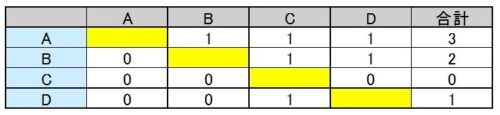
この場合、ドーナツAが勝ち点3となるので、5名の総意としてはドーナツAとなります。ドーナツB派だった2名も納得できるのではないかと。
目には見えにくい優先度を明らかにできる
上記の例だと方法およびデータ量もかなりシンプルなので、ある種「予想に近い結果」でした。しかし、もっと複雑なケースの場合だと、傍目には優勢にみえるものが実はそれほどではなかったということがクリアになることもあります。
実際に研修で行ったケースはこれとは全く違うものでした。この一対比較を使った結果、グループ内では「なんとなくこれが優勢かな」とイメージしていたものとは違うものが「実は最も優先すべきアイデア」となりました。しかし、感覚ではなく数値になって出てきたので、かなり納得感は高かったです。




